Yoselin Guarin: febrero 2011

para mi las funciones reales se trata de una funcion continiua o bien discotinuas
Una función real $f\,$ es una función matemática cuyo dominio y codominio están contenidos en $\mathbb{R}$ , es decir, es una función:

$f:S\subseteq\mathbb{R}\rightarrow S'\subseteq\mathbb{R}$

Sea

X

un conjunto cualquiera no vacío y sea ${\mathcal F}(X,{\mathbb R})$ el conjunto formado por todas las funciones de

X

en $\mathbb R$ . Muchas de las operaciones y propiedades algebraicas de los Reales se pueden extender a ${\mathcal F}(X,{\mathbb R})$ , como veremos a continuación.
Sean $f,g: X \rightarrow {\mathbb R}$ elementos de ${\mathcal F}(X,{\mathbb R})$ . Definimos operaciones entre esas funciones, punto a punto por

$f+g: x \mapsto f(x) + g(x)$ Suma de Funciones.
$f-g: x \mapsto f(x) - g(x)$ Resta de Funciones.
$fg: x \mapsto f(x)g(x)$ Producto de Funciones.

También, podemos extender relaciones punto a punto.

$f<g \iff \forall x, f(x) < g(x)$ .

La manera en que hicimos la extensión, garantiza que muchas de las propiedades de los Reales se extienden a ${\mathcal F}(X,{\mathbb R})$ . Indicamos a continuación aquellas más importantes.

La suma de funciones es asociativa, conmutativa, con neutro la función constante $x \mapsto 0$ , con opuesto aditivo $-f:x \rightarrow -f(x)\,$ para cada función f.
La resta es tal que $f - g : = f + ( - g)$ .
La multiplicación es asociativa, conmutativa, con neutro la función constante $x \mapsto 1$ , pero solamente las funciones que nunca tiene valor nulo, tienen recíprocos.
La multiplicación es distributiva respecto a la suma.

Note que todas las anteriores propiedades son análogas a propiedades de los números reales. Hay, sin embargo, propiedades "extrañas". Por ejemplo, Cuando el conjunto X tiene a lo menos dos elementos, hay divisores de cero en ${\mathcal F}(X,{\mathbb R})$ . En efecto, supongamos que

X = {a, b}

y definamos $f,g:X \rightarrow {\mathbb R}$ tales que

f (a) = 1, f (b) = 0

g (a) = 0 y g (b) = 1

. Se ve, inmediatamente, que

f g

es la función constante 0, o sea la función cero, aunque ninguno de los factores lo es.
El conjunto ${\mathcal F}(X,{\mathbb R})$ junto con sus operaciones es importante por la gran cantidad de ejemplos diversos que se obtienen al seleccionar el conjunto X.

Sea $X=\{1,2\}\,$ . Entonces, cada función de ${\mathcal F}(X,{\mathbb R})$ define una pareja de números $f (1), f (2)$ que si consideramos el orden natural en X, podemos escribir como el para ordenado $(f (1), f (2))$ . Esto nos dice que, en este caso, podemos identificar ${\mathcal F}(X,{\mathbb R})$ con el conjunto de todos los pares posibles de números reales, o sea con ${\mathbb R}^2$ .
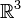Sea $X=\{1,2,3\}\,$ Razonado como arriba, podemos identificar a ${\mathcal F}(X,{\mathbb R})$ con ${\mathbb R}^3$ .
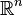Sea $X=\{1,2,3, \ldots, n\}$ Razonado como arriba, podemos identificar a ${\mathcal F}(X,{\mathbb R})$ con ${\mathbb R}^n$ .

Note que en cada uno de los ejemplos anteriores, el conjunto de pares, tríos, duplas ordenadas aparece provisto de una suma y multiplicación. La suma coincide con la suma vectorial usual y la multiplicación por constantes con la multiplicación por escalar.

Sea $X = {\mathbb N}$ , los Naturales. En este caso, ${\mathcal F}(X,{\mathbb R})$ es el conjunto de todas las sucesiones de números reales provisto como la suma y multiplicación usual de sucesiones.gracias por su atencion

Yoselin Guarin

lunes, 28 de febrero de 2011

funciones reales

miércoles, 23 de febrero de 2011

tecnoligia la informacion y la comunicacion

miércoles, 9 de febrero de 2011

bienvenidos a mi blog